Minimization¶
Minimization contents¶
One-dimensional minimizers¶
One-dimensional minimization is performed by descendants of min_base . There are four one-dimensional minimization algorithms, min_cern, min_brent_gsl, min_brent_boost, and min_quad_golden. All four are bracketing algorithms type where an interval and an initial guess must be provided. If only an initial guess and no bracket is given, these two classes will attempt to find a suitable bracket from the initial guess. While the min_base base class is designed to allow future descendants to optionally use derivative information, this is not yet supported for any one-dimensional minimizers.
Multi-dimensional minimizers¶
Multi-dimensional minimization is performed by descendants of mmin_base . O₂scl includes a simplex minimizer ( mmin_simp2), traditional minimizers which use gradient information (mmin_conp, mmin_conf, and mmin_bfgs2), and differential evolution minimizers diff_evo and diff_evo_adapt). Minimization by simulated annealing is included and described in the Simulated Annealing section. Constrained minimization is also included and described in separately in Constrained Minimization.
See an example for the usage of the multi-dimensional minimizers in the Multidimensional minimizer example below.
Simplex minimizer¶
The class mmin_simp2 minimizes a function using the Nelder-Mead simplex algorithm and does not require any information about the gradient. It is based on GSL.
Restarts of the simplex minimizer are sometimes required to find the correct minimum, and mmin_simp2 can get caught in infinite loops, especially for functions which have symmetries directly related to one or more of the parameters.
Traditional minimizers with gradient information¶
Classes mmin_conp, mmin_conf, and mmin_bfgs2 are intended for use when the gradient of the function is available, but they can also automaticallly compute the gradient numerically. The standard way to provide the gradient is to use an object of type grad_funct . The user may specify the automatic gradient object of type gradient which is used by the minimizer to compute the gradient numerically when a function is not specified.
Generally, when a closed expression is available for the gradient, mmin_bfgs2 is likely the best choice. However, the simplex methods can be more robust for sufficiently difficult functions.
It is important to note that not all of the minimization routines test the second derivative to ensure that it doesn’t vanish to ensure that we have indeed found a true minimum.
Fixing Parameters¶
The class mmin_fix_params provides a convenient way of fixing some of the parameters and minimizing over others, without requiring a the function interface to be rewritten. An example is given in the Minimizer fixing variables example below.
Multidimensional minimizer example¶
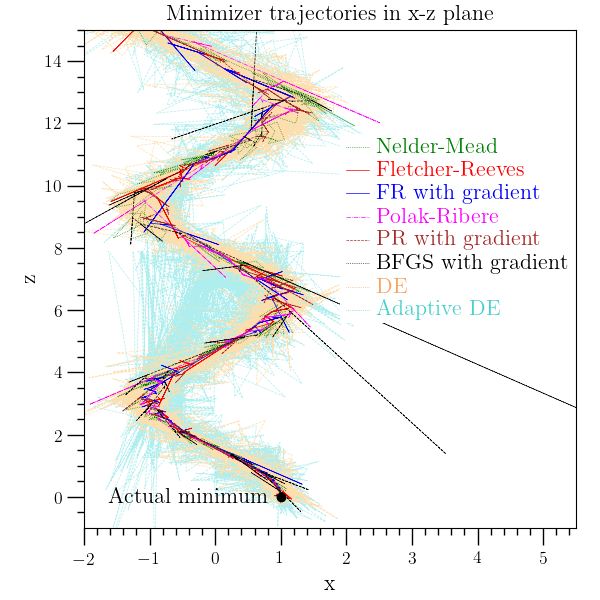
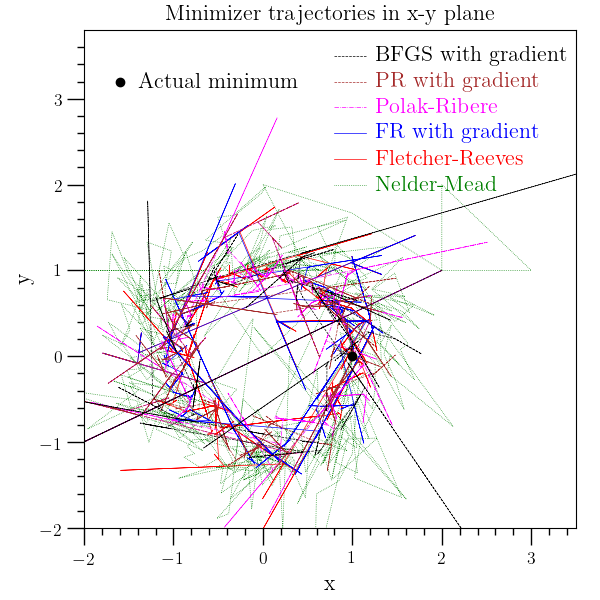
This example uses the O₂scl minimizers based on GSL to minimize a rather complicated three-dimensional function which has constant level surfaces which look like springs oriented along the z-axis. This example function, originally created here for O₂scl, was added later to the GSL library minimization test functions.
/* Example: ex_mmin.cpp
-------------------------------------------------------------------
Example usage of the multidimensional minimizers with and without
gradients. See "License Information" section of the documentation
for license information.
*/
#include <fstream>
#include <string>
#include <cmath>
#include <boost/numeric/ublas/vector.hpp>
#include <o2scl/test_mgr.h>
#include <o2scl/multi_funct.h>
#include <o2scl/constants.h>
#include <o2scl/mmin_simp2.h>
#include <o2scl/mmin_conf.h>
#include <o2scl/mmin_conp.h>
#include <o2scl/mmin_bfgs2.h>
#include <o2scl/diff_evo.h>
#include <o2scl/diff_evo_adapt.h>
#include <o2scl/rng.h>
using namespace std;
using namespace o2scl;
typedef boost::numeric::ublas::vector<double> ubvector;
class cl {
public:
cl() {
param=30.0;
rg.clock_seed();
}
/// To output function evaluations to a file
ofstream fout;
/// Parameter of the quadratic
double param;
/// Random number generator
rng<> rg;
/// Updated spring function
double spring_two(size_t nv, const ubvector &x) {
double theta=atan2(x[1],x[0]);
double r=hypot(x[0],x[1]);
double z=x[2];
double tmz=theta-z;
double fact=8.0-pow(sin(tmz+o2scl_const::pi/2.0)+1.0,3.0);
double rm1=r-1.0;
double ret=fact+exp(rm1*rm1)+z*z/param;
fout << x[0] << " " << x[1] << " " << x[2] << " " << ret << " "
<< fact << " " << rm1 << " " << endl;
return ret;
}
// Gradient of the spring function
int sgrad(size_t nv, ubvector &x, ubvector &g) {
double theta=atan2(x[1],x[0]);
double r=hypot(x[0],x[1]);
double z=x[2];
double tmz=theta-z;
double rm1=r-1.0;
double fact=8.0-pow(sin(tmz+o2scl_const::pi/2.0)+1.0,3.0);
double dtdx=-x[1]/r/r;
double dtdy=x[0]/r/r;
double drdx=x[0]/r;
double drdy=x[1]/r;
double dfdt=-3.0*pow(sin(tmz+o2scl_const::pi/2.0)+1.0,2.0)*
cos(tmz+o2scl_const::pi/2.0);
double dfdz=2.0*z/param+3.0*pow(sin(tmz+o2scl_const::pi/2.0)+1.0,2.0)*
cos(tmz+o2scl_const::pi/2.0);
double dfdr=2.0*rm1*exp(rm1*rm1);
g[0]=dfdr*drdx+dfdt*dtdx;
g[1]=dfdr*drdy+dfdt*dtdy;
g[2]=dfdz;
return 0;
}
};
int main(void) {
cl acl;
ubvector x(3);
double fmin;
test_mgr t;
t.set_output_level(1);
cout.setf(ios::scientific);
// Set up the function objects
multi_funct f1=std::bind
(std::mem_fn<double(size_t,const ubvector &)>(&cl::spring_two),
&acl,std::placeholders::_1,std::placeholders::_2);
grad_funct f1g=std::bind
(std::mem_fn<int(size_t,ubvector &,ubvector &)>(&cl::sgrad),
&acl,std::placeholders::_1,std::placeholders::_2,
std::placeholders::_3);
mmin_simp2<> gm1;
mmin_conf<> gm2;
mmin_conp<> gm3;
mmin_bfgs2<> gm4;
diff_evo<> gm5;
diff_evo_adapt<> gm6;
vector<double> guess={2.0,1.0,7.0*o2scl_const::pi};
// This function is difficult to minimize, so more trials
// are required.
gm1.ntrial*=10;
gm2.ntrial*=10;
gm3.ntrial*=10;
gm4.ntrial*=10;
// Simplex minimization
acl.fout.open("data/ex_mmin1.dat");
vector_copy(3,guess,x);
gm1.mmin(3,x,fmin,f1);
acl.fout.close();
cout << gm1.last_ntrial << endl;
cout << "Found minimum at: "
<< x[0] << " " << x[1] << " " << x[2] << endl;
t.test_rel(x[0],1.0,1.0e-4,"1a");
t.test_rel(x[1],0.0,1.0e-4,"1b");
t.test_rel(x[2],0.0,1.0e-4,"1c");
// Fletcher-Reeves conjugate
acl.fout.open("data/ex_mmin2.dat");
vector_copy(3,guess,x);
gm2.mmin(3,x,fmin,f1);
acl.fout.close();
cout << gm2.last_ntrial << endl;
cout << "Found minimum at: "
<< x[0] << " " << x[1] << " " << x[2] << endl;
t.test_rel(x[0],1.0,4.0e-3,"2a");
t.test_rel(x[1],0.0,4.0e-3,"2b");
t.test_rel(x[2],0.0,4.0e-3,"2c");
// Fletcher-Reeves conjugate with gradients
acl.fout.open("data/ex_mmin2g.dat");
vector_copy(3,guess,x);
gm2.mmin_de(3,x,fmin,f1,f1g);
acl.fout.close();
cout << gm2.last_ntrial << endl;
cout << "Found minimum at: "
<< x[0] << " " << x[1] << " " << x[2] << endl;
t.test_rel(x[0],1.0,4.0e-3,"2ga");
t.test_rel(x[1],0.0,4.0e-3,"2gb");
t.test_rel(x[2],0.0,4.0e-3,"2gc");
// Polak-Ribere conjugate
acl.fout.open("data/ex_mmin3.dat");
vector_copy(3,guess,x);
gm3.mmin(3,x,fmin,f1);
acl.fout.close();
cout << gm3.last_ntrial << endl;
cout << "Found minimum at: "
<< x[0] << " " << x[1] << " " << x[2] << endl;
t.test_rel(x[0],1.0,4.0e-3,"3a");
t.test_rel(x[1],0.0,4.0e-3,"3b");
t.test_rel(x[2],0.0,4.0e-3,"3c");
// Polak-Ribere conjugate with gradients
acl.fout.open("data/ex_mmin3g.dat");
vector_copy(3,guess,x);
gm3.mmin_de(3,x,fmin,f1,f1g);
acl.fout.close();
cout << gm3.last_ntrial << endl;
cout << "Found minimum at: "
<< x[0] << " " << x[1] << " " << x[2] << endl;
t.test_rel(x[0],1.0,4.0e-3,"3ga");
t.test_rel(x[1],0.0,4.0e-3,"3gb");
t.test_rel(x[2],0.0,4.0e-3,"3gc");
// de
acl.fout.open("data/ex_mmin5.dat");
vector_copy(3,guess,x);
gm5.mmin(3,x,fmin,f1);
acl.fout.close();
cout << gm5.last_ntrial << endl;
cout << "Found minimum at: "
<< x[0] << " " << x[1] << " " << x[2] << endl;
// AWS, 7/23/22: this method sometimes fails so increasing
// tolerances
t.test_rel(x[0],1.0,4.0e0,"5a");
t.test_rel(x[1],0.0,4.0e0,"5b");
t.test_rel(x[2],0.0,4.0e0,"5c");
// dea
// 7/17/25: This algorithm can be more unpredictable
acl.fout.open("data/ex_mmin6.dat");
vector_copy(3,guess,x);
gm6.mmin(3,x,fmin,f1);
acl.fout.close();
cout << gm6.last_ntrial << endl;
cout << "Found minimum at: "
<< x[0] << " " << x[1] << " " << x[2] << endl;
t.test_rel(x[0],1.0,10.0,"6a");
t.test_rel(x[1],0.0,10.0,"6b");
t.test_rel(x[2],0.0,10.0,"6c");
t.report();
return 0;
}
/*
The BFGS minimizer doesn't appear to work for this particular
example. This may be a result of finite precision in the object
function rather than a failure of the BFGS.
// BFGS with gradients
acl.fout.open("ex_mmin4g.dat");
vector_copy(3,guess,x);
gm4.mmin_de(3,x,fmin,f1,f1g);
acl.fout.close();
cout << gm4.last_ntrial << endl;
cout << "Found minimum at: "
<< x[0] << " " << x[1] << " " << x[2] << endl;
t.test_rel(x[0],1.0,4.0e-3,"4ga");
t.test_rel(x[1],0.0,4.0e-3,"4gb");
t.test_rel(x[2],0.0,4.0e-3,"4gc");
gm4.def_grad.epsrel=1.0e-8;
acl.fout.open("ex_mmin4.dat");
vector_copy(3,guess,x);
gm4.mmin(3,x,fmin,f1);
acl.fout.close();
cout << gm4.last_ntrial << endl;
cout << "Found minimum at: "
<< x[0] << " " << x[1] << " " << x[2] << endl;
t.test_rel(x[0],1.0,4.0e-3,"4a");
t.test_rel(x[1],0.0,4.0e-3,"4b");
t.test_rel(x[2],0.0,4.0e-3,"4c");
*/
Minimizer fixing variables example¶
This example uses the mmin_fix_params class to minimize the function
while fixing some of the parameters.
/* Example: ex_mmin_fix.cpp
-------------------------------------------------------------------
Example usage of the mmin_fix class, which fixes some of the
paramters for a multidimensional minimization. See "License
Information" section of the documentation for license information.
*/
#include <cmath>
#include <boost/numeric/ublas/vector.hpp>
#include <o2scl/test_mgr.h>
#include <o2scl/multi_funct.h>
#include <o2scl/mmin_simp2.h>
#include <o2scl/mmin_fix.h>
using namespace std;
using namespace o2scl;
typedef boost::numeric::ublas::vector<double> ubvector;
class cl {
public:
double mfn(size_t nv, const ubvector &x) {
return (x[0]-2.0)*(x[0]-2.0)+(x[1]-1.0)*(x[1]-1.0)+x[2]*x[2];
}
};
int main(void) {
cl acl;
ubvector x(3);
double fmin;
test_mgr t;
t.set_output_level(1);
cout.setf(ios::scientific);
/*
Perform the minimization the standard way, with the
simplex2 minimizer
*/
multi_funct f1c11=
std::bind(std::mem_fn<double(size_t,const ubvector &)>(&cl::mfn),
&acl,std::placeholders::_1,std::placeholders::_2);
mmin_simp2<> gm1;
x[0]=0.5;
x[1]=0.5;
x[2]=0.5;
gm1.mmin(3,x,fmin,f1c11);
cout << gm1.last_ntrial << " iterations." << endl;
cout << "Found minimum at: "
<< x[0] << " " << x[1] << " " << x[2] << endl;
t.test_rel(x[0],2.0,1.0e-4,"1a");
t.test_rel(x[1],1.0,1.0e-4,"1b");
t.test_rel(x[2],0.0,1.0e-4,"1c");
// Create a new mmin_fix_params object
mmin_fix_params<> gmf;
// Create a base minimizer which can be used by the mmin_fix_params
// object. Note that we can't use 'gm1' here, because it has a
// different type than 'gm2', even though its functionality is
// effectively the same.
mmin_simp2<mmin_fix_params<> > gm2;
// Set the base minimizer
gmf.set_mmin(gm2);
/*
First perform the minimization as above.
*/
x[0]=0.5;
x[1]=0.5;
x[2]=0.5;
gmf.mmin(3,x,fmin,f1c11);
cout << gmf.last_ntrial << " iterations." << endl;
cout << "Found minimum at: "
<< x[0] << " " << x[1] << " " << x[2] << endl;
t.test_rel(x[0],2.0,1.0e-4,"2a");
t.test_rel(x[1],1.0,1.0e-4,"2b");
t.test_rel(x[2],0.0,1.0e-4,"2c");
/*
Now fix the 2nd variable, and re-minimize.
*/
bool fix[3]={false,true,false};
x[0]=0.5;
x[1]=0.5;
x[2]=0.5;
gmf.mmin_fix(3,x,fmin,fix,f1c11);
cout << gmf.last_ntrial << " iterations." << endl;
cout << "Found minimum at: "
<< x[0] << " " << x[1] << " " << x[2] << endl;
t.test_rel(x[0],2.0,1.0e-4,"3a");
t.test_rel(x[1],0.5,1.0e-4,"3b");
t.test_rel(x[2],0.0,1.0e-4,"3c");
t.report();
return 0;
}