Simulated Annealing

O2scl

Simulated annealing contents

• Simulated annealing introduction

• Simulated annealing example

Simulated annealing introduction

Minimization by simulated annealing is performed by a modified version of the GSL algorithm in the anneal_gsl class. A version which includes OpenMP and MPI parallelization is provided in anneal_para.

Simulated annealing example

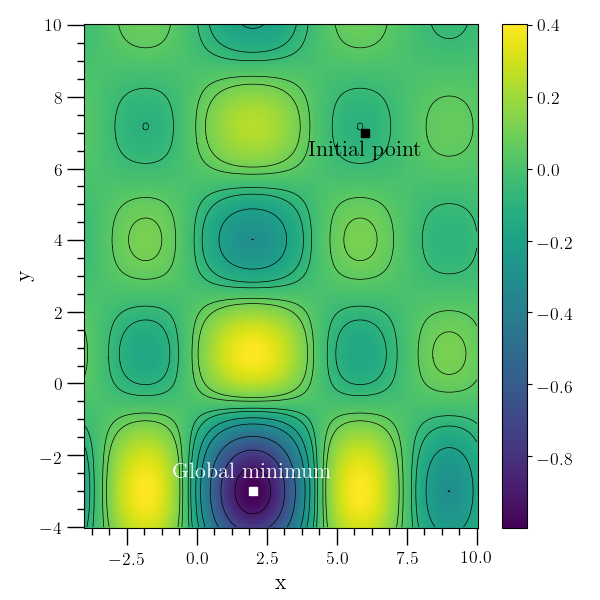
This example minimizes the function

\[f(x,y) = J_0(x-2) J_0(y+3)\]

over \((x,y)\) where \(J_0(x)\) is the Bessel function given in gsl_sf_bessel_J0. The initial guess at \((9,9)\) is far away from the global minimum.

The plot below plots the function above, the initial guess, and the minimum obtained by the example program.

/* Example: ex_anneal.cpp
   -------------------------------------------------------------------
   An example to demonstrate minimization by simulated annealing. See 
   "License Information" section of the documentation for license 
   information.
*/
  
#include <iostream>
#include <cmath>
#include <boost/numeric/ublas/vector.hpp>
#include <gsl/gsl_sf_bessel.h>
#include <o2scl/multi_funct.h>
#include <o2scl/funct.h>
#include <o2scl/anneal_gsl.h>
#include <o2scl/test_mgr.h>
#include <o2scl/hdf_file.h>
#include <o2scl/hdf_io.h>

using namespace std;
using namespace o2scl;
using namespace o2scl_hdf;

typedef boost::numeric::ublas::vector<double> ubvector;

// Make data for the plot in the documentation
void make_plot_data();

// A simple function with many local minima. A "greedy" minimizer
// would likely fail to find the correct minimum.
double bessel_fun(size_t nvar, const ubvector &x) {

  double a, b;
  a=(x[0]-2.0);
  b=(x[1]+3.0);

  // This is important to prevent the annealing algorithm to
  // random walk to infinity since the product of Bessel
  // functions is flat far from the origin
  if (fabs(x[0])>10.0 || fabs(x[1])>10.0) return 10.0;

  return -gsl_sf_bessel_J0(a)*gsl_sf_bessel_J0(b);
}

int main(int argc, char *argv[]) {
  cout.setf(ios::scientific);
  
  test_mgr t;
  t.set_output_level(1);

  anneal_gsl<> ga;
  double result;
  ubvector init(2);
  
  multi_funct fx=bessel_fun;
  
  ga.ntrial=4000;
  ga.verbose=1;
  ga.tol_abs=1.0e-7;
  ga.T_dec=1.1;

  // Set a large initial step size
  double step[1]={10.0};
  ga.set_step(1,step);

  // Choose an initial point at a local minimum away from
  // the global minimum
  init[0]=6.0;
  init[1]=7.0;
  
  // Perform the minimization
  ga.mmin(2,init,result,fx);
  cout << "x: " << init[0] << " " << init[1] 
       << ", minimum function value: " << result << endl;
  cout << endl;

  // Test that it found the global minimum
  t.test_rel(init[0],2.0,8.0e-2,"another test - value");
  t.test_rel(init[1],-3.0,1.0e-2,"another test - value 2");
  t.test_rel(result,-1.0,1.0e-3,"another test - min");

  make_plot_data();
  
  t.report();
  
  return 0;
}

void make_plot_data() {
  table3d t3d;
  uniform_grid_end<double> ug(-4.0,10.0,199);
  t3d.set_xy("x",ug,"y",ug);
  t3d.new_slice("f");
  for(size_t i=0;i<t3d.get_nx();i++) {
    for(size_t j=0;j<t3d.get_ny();j++) {
      ubvector v(2);
      v[0]=ug[i];
      v[1]=ug[j];
      t3d.set(i,j,"f",bessel_fun(2,v));
    }
  }
  hdf_file hf;
  hf.open_or_create("ex_anneal_plot.o2");
  hdf_output(hf,(const table3d &)t3d,"ex_anneal");
  hf.close();
  return;
}