Probability Distributions and Markov Chain Monte Carlo¶
MCMC Contents¶
Probability distributions¶
Probability distributions are provided by the C++ standard library, but some useful functionality is not included and multidimensional and conditional distributions are not provided. For the time being, some experimental probability distributions are included in O₂scl.
The one-dimensional probability distributions are children of prob_dens_func and are modeled similar to the C++ standard distributions:
Multi-dimensional distributions are children of prob_dens_mdim, including
Conditional probability distributions are children of prob_cond_mdim. These classes can be used as proposal distributions for the O₂scl MCMC classes.
Markov chain Monte Carlo (MCMC)¶
The class mcmc_para_base performs generic MCMC simulations and the child class mcmc_para_table performs MCMC simulations and stores the results in a table_units object. These classes contain support for OpenMP and MPI (or both). The class mcmc_para_cli is a specialized class which automatically handles the command-line interface when using MCMC.
MCMC example¶
The first example shows an MCMC of a bimodal distribution,
\[f(x) = \exp ( -x^2) \left[ \sin \left( x-7/5 \right) + 1 \right]\]
with a naive random walk step. It uses that MCMC to compute the value
\[\left< x^2 \right> = \left( \int_{-5}^{5} x^2 f(x) \right)
\left( \int_{-5}^{5} f(x) \right)^{-1}\]
and compares that value with the exact result obtained by quadrature.
/* Example: ex_mcmc.cpp
───────────────────────────────────────────────────────────────────
An example which demonstrates the generation of an arbitrary
distribution through Markov chain Monte Carlo. See "License
Information" section of the documentation for license information.
*/
#include <o2scl/mcmc_para.h>
#include <o2scl/vec_stats.h>
#include <o2scl/test_mgr.h>
#include <o2scl/hdf_io.h>
#include <o2scl/inte_qag_gsl.h>
using namespace std;
using namespace o2scl;
using namespace o2scl_hdf;
/// Convenient typedefs
typedef boost::numeric::ublas::vector<double> ubvector;
typedef boost::numeric::ublas::matrix<double> ubmatrix;
typedef std::function<int(size_t,const ubvector &,double &,
std::vector<double> &)> point_funct;
typedef std::function<int(const ubvector &,double,std::vector<double> &,
std::vector<double> &)> fill_funct;
/// The MCMC object
mcmc_para_table<point_funct,fill_funct,std::vector<double>,ubvector> mct;
/** \brief A demonstration class for the MCMC example. This example
could have been written with global functions, but we put them
in a class to show how it would work in that case.
*/
class exc {
public:
/** \brief A one-dimensional bimodal distribution
Here, the variable 'log_weight' stores the natural logarithm of
the objective function based on the parameters stored in \c pars.
The object 'dat' stores any auxillary quantities which can be
computed at every point in parameter space.
*/
int bimodal(size_t nv, const ubvector &pars, double &log_weight,
std::vector<double> &dat) {
double x=pars[0];
log_weight=log(exp(-x*x)*(sin(x-1.4)+1.0));
dat[0]=x*x;
return 0;
}
/** \brief Add auxillary quantities to 'line' so they can be
stored in the table
*/
int fill_line(const ubvector &pars, double log_weight,
std::vector<double> &line, std::vector<double> &dat) {
line.push_back(dat[0]);
return 0;
}
exc() {
}
};
int main(int argc, char *argv[]) {
cout.setf(ios::scientific);
exc e;
test_mgr tm;
tm.set_output_level(1);
// Parameter limits and initial points
ubvector low_bimodal(1), high_bimodal(1);
low_bimodal[0]=-5.0;
high_bimodal[0]=5.0;
// Function objects for the MCMC object
point_funct bimodal_func=std::bind
(std::mem_fn<int(size_t,const ubvector &,double &,
std::vector<double> &)>(&exc::bimodal),&e,
std::placeholders::_1,std::placeholders::_2,std::placeholders::_3,
std::placeholders::_4);
fill_funct fill_func=std::bind
(std::mem_fn<int(const ubvector &,double,std::vector<double> &,
std::vector<double> &)>(&exc::fill_line),&e,
std::placeholders::_1,std::placeholders::_2,std::placeholders::_3,
std::placeholders::_4);
// Create function object vectors
vector<point_funct> bimodal_vec;
bimodal_vec.push_back(bimodal_func);
vector<fill_funct> fill_vec;
fill_vec.push_back(fill_func);
// Create and allocate data objects
vector<std::vector<double> > data_vec(2);
data_vec[0].resize(1);
data_vec[1].resize(1);
// Compute exact value of <x^2>. The function format is a bit
// different so we use lambda expressions to construct the
// functions for the integrators.
inte_qag_gsl<> iqg;
funct f=[e,data_vec](double x) mutable -> double {
ubvector u(1); double lw; u[0]=x;
e.bimodal(1,u,lw,data_vec[0]); return exp(lw); };
funct fx2=[e,data_vec](double x) mutable -> double {
ubvector u(1); double lw; u[0]=x;
e.bimodal(1,u,lw,data_vec[0]); return data_vec[0][0]*exp(lw); };
cout << iqg.integ(fx2,low_bimodal[0],high_bimodal[0]) << " "
<< iqg.integ(f,low_bimodal[0],high_bimodal[0]) << endl;
double exact=iqg.integ(fx2,low_bimodal[0],high_bimodal[0])/
iqg.integ(f,low_bimodal[0],high_bimodal[0]);
cout << "exact: " << exact << endl;
cout << "──────────────────────────────────────────────────────────"
<< endl;
cout << "Plain MCMC example with a bimodal distribution:" << endl;
// Set parameter names and units
vector<string> pnames={"x","x2"};
vector<string> punits={"",""};
mct.set_names_units(pnames,punits);
// Set MCMC parameters
mct.stepper.step_fac.resize(1);
mct.stepper.step_fac[0]=2.0;
mct.max_iters=20000;
mct.prefix="ex_mcmc";
mct.table_prealloc=mct.max_iters/3;
// Perform MCMC
mct.mcmc_fill(1,low_bimodal,high_bimodal,bimodal_vec,fill_vec,
data_vec);
// Output acceptance and rejection rate
cout << "n_accept, n_reject: " << mct.n_accept[0] << " "
<< mct.n_reject[0] << endl;
// Get the MCMC results
shared_ptr<table_units<> > t=mct.get_table();
// Remove empty rows from table
t->delete_rows_func("mult<0.5");
// Compute the autocorrelation length
std::vector<double> ac, ftom;
o2scl::vector_autocorr_vector_mult(t->get_nlines(),
(*t)["x2"],(*t)["mult"],ac);
size_t ac_len=o2scl::vector_autocorr_tau(ac,ftom);
// Create a separate table of statistically independent samples
table_units<> indep;
copy_table_thin_mcmc(ac_len,*t,indep,"mult");
cout << "Autocorrelation length, effective sample size: "
<< ac_len << " " << indep.get_nlines() << endl;
// Write the data to a file
hdf_file hf;
hf.open_or_create("ex_mcmc.o2");
hdf_output(hf,*t,"mcmc");
hdf_output(hf,indep,"indep");
hf.close();
// Use the independent samples to compute the final integral and
// compare to the exact result. Note that we must specify the
// number of elements in the vector, indep["x2"], because the
// table_units object often has space at the end to add extra rows.
double avg=vector_mean(indep.get_nlines(),indep["x2"]);
double std=vector_stddev(indep.get_nlines(),indep["x2"]);
tm.test_rel(avg,exact,10.0*std/sqrt(indep.get_nlines()),"ex_mcmc");
cout << "avg. from MCMC, exact avg., diff., std. from MCMC, "
<< "unc. in mean times 10:\n "
<< avg << " " << exact << " " << fabs(avg-exact) << " "
<< std << " " << 10.0*std/sqrt(indep.get_nlines()) << endl;
tm.report();
return 0;
}
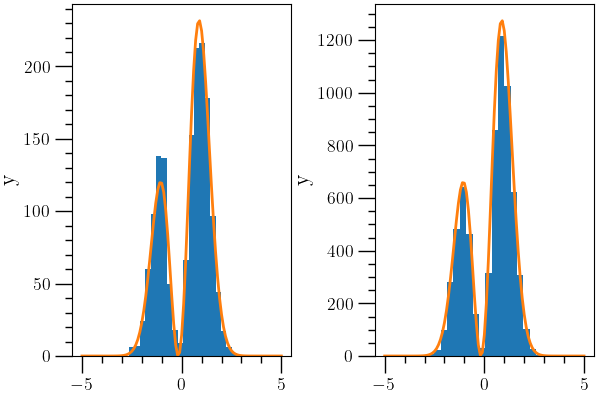
The image plots the posterior distribution from this first MCMC as well as a second MCMC using a proposal distribution generated from a kernel density estimation (from the kde_python class) of the data generated from the first MCMC. This simulation is about five times more efficient, and thus gives a more accurate result for the integral.
Below is the code for the second MCMC, which uses O₂scl C++ interface to SciPy’s KDE algorithm.
/* Example: ex_mcmc_kde.cpp
───────────────────────────────────────────────────────────────────
An example which demonstrates the generation of an arbitrary
distribution through Markov chain Monte Carlo using a conditional
probability distribution built using a KDE applied to previous
data. See "License Information" section of the documentation for
license information.
*/
#include <o2scl/mcmc_para.h>
#include <o2scl/vec_stats.h>
#include <o2scl/test_mgr.h>
#include <o2scl/hdf_io.h>
#include <o2scl/inte_qag_gsl.h>
#include <o2scl/set_openmp.h>
#include <o2scl/kde_python.h>
using namespace std;
using namespace o2scl;
using namespace o2scl_hdf;
/// Convenient typedefs
typedef boost::numeric::ublas::vector<double> ubvector;
typedef boost::numeric::ublas::matrix<double> ubmatrix;
typedef std::function<int(size_t,const ubvector &,double &,
std::vector<double> &)> point_funct;
typedef std::function<int(const ubvector &,double,std::vector<double> &,
std::vector<double> &)> fill_funct;
/// The MCMC object
mcmc_para_table<point_funct,fill_funct,std::vector<double>,ubvector,
mcmc_stepper_mh<point_funct,std::vector<double>,
ubvector,ubmatrix,
prob_cond_mdim_indep<>>> mct;
/** \brief A demonstration class for the MCMC example. This example
could have been written with global functions, but we put them
in a class to show how it would work in that case.
*/
class exc {
public:
/** \brief A one-dimensional bimodal distribution
Here, the variable 'log_weight' stores the natural logarithm of
the objective function based on the parameters stored in \c pars.
The object 'dat' stores any auxillary quantities which can be
computed at every point in parameter space.
*/
int bimodal(size_t nv, const ubvector &pars, double &log_weight,
std::vector<double> &dat) {
double x=pars[0];
log_weight=log(exp(-x*x)*(sin(x-1.4)+1.0));
dat[0]=x*x;
return 0;
}
/** \brief Add auxillary quantities to 'line' so they can be
stored in the table
*/
int fill_line(const ubvector &pars, double log_weight,
std::vector<double> &line, std::vector<double> &dat) {
line.push_back(dat[0]);
return 0;
}
exc() {
}
};
int main(int argc, char *argv[]) {
cout.setf(ios::scientific);
exc e;
test_mgr tm;
tm.set_output_level(1);
// Parameter limits and initial points
ubvector low_bimodal(1), high_bimodal(1);
low_bimodal[0]=-5.0;
high_bimodal[0]=5.0;
// Function objects for the MCMC object
point_funct bimodal_func=std::bind
(std::mem_fn<int(size_t,const ubvector &,double &,
std::vector<double> &)>(&exc::bimodal),&e,
std::placeholders::_1,std::placeholders::_2,std::placeholders::_3,
std::placeholders::_4);
fill_funct fill_func=std::bind
(std::mem_fn<int(const ubvector &,double,std::vector<double> &,
std::vector<double> &)>(&exc::fill_line),&e,
std::placeholders::_1,std::placeholders::_2,std::placeholders::_3,
std::placeholders::_4);
// Create function object vectors
vector<point_funct> bimodal_vec;
bimodal_vec.push_back(bimodal_func);
vector<fill_funct> fill_vec;
fill_vec.push_back(fill_func);
// Create and allocate data objects
vector<std::vector<double> > data_vec(2);
data_vec[0].resize(1);
data_vec[1].resize(1);
// Compute exact value of <x^2>. The function format is a bit
// different so we use lambda expressions to construct the
// functions for the integrators.
inte_qag_gsl<> iqg;
funct f=[e,data_vec](double x) mutable -> double {
ubvector u(1); double lw; u[0]=x;
e.bimodal(1,u,lw,data_vec[0]); return exp(lw); };
funct fx2=[e,data_vec](double x) mutable -> double {
ubvector u(1); double lw; u[0]=x;
e.bimodal(1,u,lw,data_vec[0]); return data_vec[0][0]*exp(lw); };
double exact=iqg.integ(fx2,low_bimodal[0],high_bimodal[0])/
iqg.integ(f,low_bimodal[0],high_bimodal[0]);
cout << "exact: " << exact << endl;
cout << "──────────────────────────────────────────────────────────"
<< endl;
cout << "Plain MCMC example with a bimodal distribution:" << endl;
// Set parameter names and units
vector<string> pnames={"x","x2"};
vector<string> punits={"",""};
mct.set_names_units(pnames,punits);
// Read the preliminary data from a file
hdf_file hf;
hf.open("ex_mcmc.o2");
table_units<> tab_in;
hdf_input(hf,tab_in,"indep");
hf.close();
// Copy the table data to a tensor for use in kde_python.
// We need a copy for each thread because kde_python takes
// over the tensor data.
tensor<> ten_in;
vector<size_t> in_size={tab_in.get_nlines(),1};
ten_in.resize(2,in_size);
for(size_t i=0;i<tab_in.get_nlines();i++) {
vector<size_t> ix;
ix={i,0};
ten_in.get(ix)=tab_in.get("x",i);
}
// Train the KDE
vector<double> weights;
std::shared_ptr<kde_python<ubvector>> kp(new kde_python<ubvector>);
kp->set_function("o2sclpy",ten_in,
weights,"verbose=0","kde_scipy");
// Setting the KDE as the base distribution for the independent
// conditional probability.
mct.stepper.proposal.resize(1);
mct.stepper.proposal[0].set_base(kp);
// Set the MCMC parameters
mct.max_iters=20000;
mct.prefix="ex_mcmc_kde";
mct.n_threads=1;
mct.verbose=3;
// Perform MCMC
mct.mcmc_fill(1,low_bimodal,high_bimodal,bimodal_vec,fill_vec,
data_vec);
// Output acceptance and rejection rate
cout << "n_accept, n_reject: " << mct.n_accept[0] << " "
<< mct.n_reject[0] << endl;
// Get results
shared_ptr<table_units<> > t=mct.get_table();
// Remove empty rows from table.
t->delete_rows_func("mult<0.5");
// Compute the autocorrelation length
std::vector<double> ac, ftom;
o2scl::vector_autocorr_vector_mult(t->get_nlines(),
(*t)["x2"],(*t)["mult"],ac);
size_t ac_len=o2scl::vector_autocorr_tau(ac,ftom);
// Create a separate table of statistically independent samples
table_units<> indep;
copy_table_thin_mcmc(ac_len,*t,indep,"mult");
cout << "Autocorrelation length, effective sample size: "
<< ac_len << " " << indep.get_nlines() << endl;
// Write these samples to a file
hf.open_or_create("ex_mcmc_kde.o2");
hdf_output(hf,*t,"mcmc");
hdf_output(hf,indep,"indep");
hf.close();
// Compute the average of the correlated samples for comparison
double avg2=vector_mean(t->get_nlines(),(*t)["x2"]);
cout << "Average of correlated samples: " << avg2 << endl;
// Use the independent samples to compute the final integral and
// compare to the exact result. Note that we must specify the
// number of elements in the vector, indep["x2"], because the
// table_units object often has space at the end to add extra rows.
double avg=vector_mean(indep.get_nlines(),indep["x2"]);
double std=vector_stddev(indep.get_nlines(),indep["x2"]);
cout << "Average and std. dev. of uncorrelated samples: "
<< avg << " " << std << endl;
cout << "Absolute difference: " << fabs(avg-exact) << endl;
cout << "Uncertainty in the average: "
<< std/sqrt(indep.get_nlines()) << endl;
tm.test_rel(avg,exact,10.0*std/sqrt(indep.get_nlines()),"ex_mcmc");
tm.report();
return 0;
}