Higher-dimensional Interpolation¶
Higher-dimensional Interpolation Contents¶
Two-dimensional interpolation¶
There are two types of two-dimensional interpolation classes, the first is based on a function defined on a two-dimensional grid (though the spacings between grid points need not be equal). The class interp2_direct implements bilinear or bicubic interpolation, and is based on D. Zaslavsky’s routines at https://github.com/diazona/interp2d (licensed under GPLv3). A slightly slower (but a bit more flexible) alternative is successive use of interp_base objects, implemented in interp2_seq .
If data is arranged without a grid, then you can either use one of the multi-dimensional interpolation classes described below or interp2_neigh, which performs nearest-neighbor interpolation. At present, contour lines can only be computed with data which is defined on a grid.
Multi-dimensional interpolation¶
There are three classes for multi-dimensional interpolation of data (where the independent variables may or may not be defined on a grid). Multidimensional-dimensional kriging (Gaussian process interpolation) is performed by interpm_krige_optim . Eigen and Armadillo specifications are also available (see Interpolation specializations). A C++ interface for interpolation in Python using several different methods including Gaussian processes or neural networks from O₂sclpy is provided in interpm_python when Python support is enabled. Finally, inverse distance weighted interpolation is performed by interpm_idw. These interpolation classes are all built upon interpm_base.
Multi-dimensional interpolation for data defined on a grid is
possible with tensor_grid. See the documentation
for o2scl::tensor_grid::interpolate(),
o2scl::tensor_grid::interp_linear() and
o2scl::tensor_grid::rearrange_and_copy(). Also, if you
want to interpolate rank-1 indices to get a vector result, you can
use o2scl::tensor_grid::interp_linear_vec() .
Interpolation specializations¶
Warning
doxygentypedef: Cannot find typedef “interpm_krige_optim_eigen” in doxygen xml output for project “o2scl” from directory: /home/awsteiner/wcs/o2scl/doc/o2scl/xml
Warning
doxygentypedef: Cannot find typedef “interpm_krige_optim_arma” in doxygen xml output for project “o2scl” from directory: /home/awsteiner/wcs/o2scl/doc/o2scl/xml
Interpolation on a rectangular grid¶
/* Example: ex_interp2.cpp
-------------------------------------------------------------------
A simple example for two-dimensional interpolation using
the interp_twod class.
*/
#include <boost/numeric/ublas/vector.hpp>
#include <boost/numeric/ublas/matrix.hpp>
#include <o2scl/interp2_seq.h>
#include <o2scl/test_mgr.h>
using namespace std;
using namespace o2scl;
// A function for filling the data and comparing results
double f(double x, double y) {
return pow(sin(0.1*x+0.3*y),2.0);
}
int main(void) {
cout.setf(ios::scientific);
test_mgr t;
t.set_output_level(1);
int i,j;
typedef boost::numeric::ublas::vector<double> ubvector;
typedef boost::numeric::ublas::matrix<double> ubmatrix;
typedef boost::numeric::ublas::matrix_row<ubmatrix> ubmatrix_row;
// Create the sample data
ubvector x(3), y(3);
ubmatrix data(3,3);
// Set the grid
x[0]=0.0;
x[1]=1.0;
x[2]=2.0;
y[0]=3.0;
y[1]=2.0;
y[2]=1.0;
// Set and print out the data
cout << endl;
cout << "Data: " << endl;
cout << " x | ";
for(i=0;i<3;i++) cout << x[i] << " ";
cout << endl;
cout << " y |" << endl;
cout << "-------------|-";
for(i=0;i<3;i++) cout << "-------------";
cout << endl;
for(i=0;i<3;i++) {
cout << y[i] << " | ";
for(j=0;j<3;j++) {
data(i,j)=f(x[j],y[i]);
cout << data(i,j) << " ";
}
cout << endl;
}
cout << endl;
// Perform the interpolation
cout << "x y Calc. Exact" << endl;
interp2_seq<ubvector,ubmatrix,ubmatrix_row> ti;
// Interpolation, x-first
double tol=0.05;
double tol2=0.4;
ti.set_data(3,3,x,y,data,itp_cspline);
double x0, y0, x1, y1;
x0=0.5; y0=1.5;
cout << x0 << " " << y0 << " "
<< ti.eval(x0,y0) << " " << f(x0,y0) << endl;
x0=0.99; y0=1.99;
cout << x0 << " " << y0 << " "
<< ti.eval(x0,y0) << " " << f(x0,y0) << endl;
x0=1.0; y0=2.0;
cout << x0 << " " << y0 << " "
<< ti.eval(x0,y0) << " " << f(x0,y0) << endl;
cout << endl;
// Interpolation, y-first
ti.set_data(3,3,x,y,data,itp_cspline);
x0=0.5; y0=1.5;
cout << x0 << " " << y0 << " "
<< ti.eval(x0,y0) << " " << f(x0,y0) << endl;
x0=0.99; y0=1.99;
cout << x0 << " " << y0 << " "
<< ti.eval(x0,y0) << " " << f(x0,y0) << endl;
x0=1.0; y0=2.0;
cout << x0 << " " << y0 << " "
<< ti.eval(x0,y0) << " " << f(x0,y0) << endl;
cout << endl;
t.report();
return 0;
}
// End of example
This example creates a sample 3 by 3 grid of data with the function \(\left[ \sin \left( x/10 + 3 y/10 \right) \right]^2\) and performs some interpolations and compares them with the exact result.
Data:
x | 0.000000e+00 1.000000e+00 2.000000e+00
y |
-------------|----------------------------------------
3.000000e+00 | 6.136010e-01 7.080734e-01 7.942506e-01
2.000000e+00 | 3.188211e-01 4.150164e-01 5.145998e-01
1.000000e+00 | 8.733219e-02 1.516466e-01 2.298488e-01
x y Calc. Exact
5.000000e-01 1.500000e+00 6.070521e-01 2.298488e-01
9.900000e-01 1.990000e+00 4.187808e-01 4.110774e-01
1.000000e+00 2.000000e+00 4.150164e-01 4.150164e-01
5.000000e-01 1.500000e+00 6.070521e-01 2.298488e-01
9.900000e-01 1.990000e+00 4.187808e-01 4.110774e-01
1.000000e+00 2.000000e+00 4.150164e-01 4.150164e-01
0 tests performed.
All tests passed.
Contour lines¶
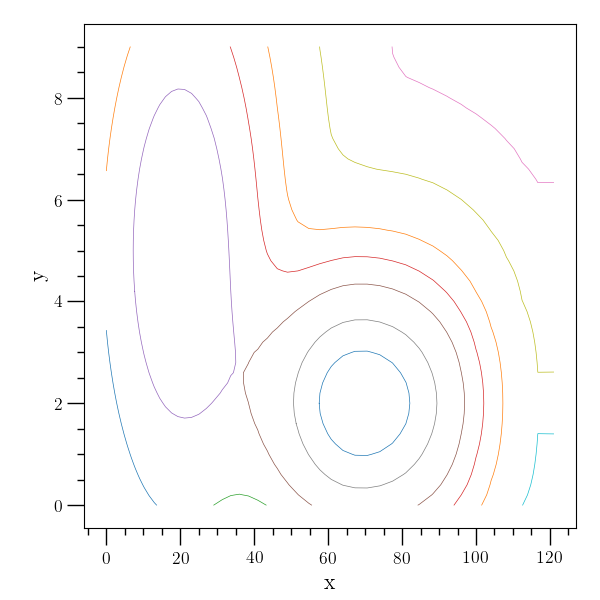
This example generates contour lines of the function
The figure below shows contour lines in the region \(x\in(0,121), y\in(0,9)\). The data grid is represented by plus signs, and the associated generated contours. The figure clearly shows the peaks at \((20,5)\) and \((70,2)\).
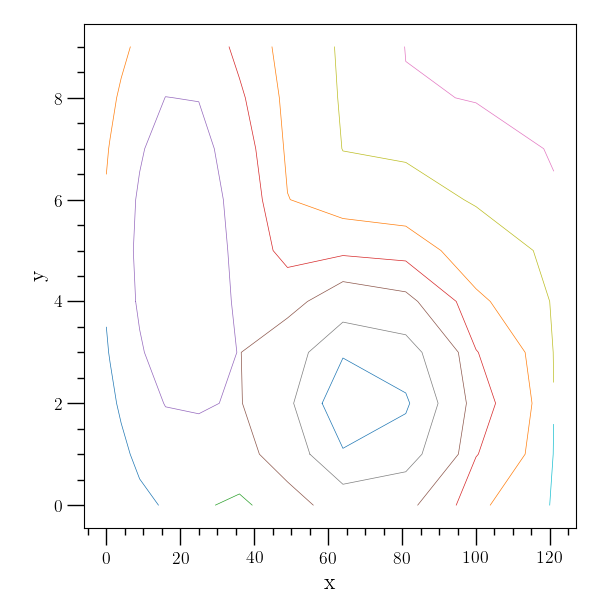
The contour class can also use interpolation to attempt to refine the data grid. The new contours after a refinement of a factor of 5 is given in the figure below.