Chebyshev Approximation

O2scl

Chebyshev Approximation Contents

• Chebyshev approximation introduction

• Chebyshev approximation example

Chebyshev approximation introduction

A class implementing the Chebyshev approximations based on GSL is given in cheb_approx_tl. This class has its own copy constructor, so that Chebyshev approximations can be copied and passed as arguments to functions. Derivatives and integrals of cheb_approx_tl objects are created as new cheb_approx_tl objects which can be easily manipulated.

Chebyshev approximation example

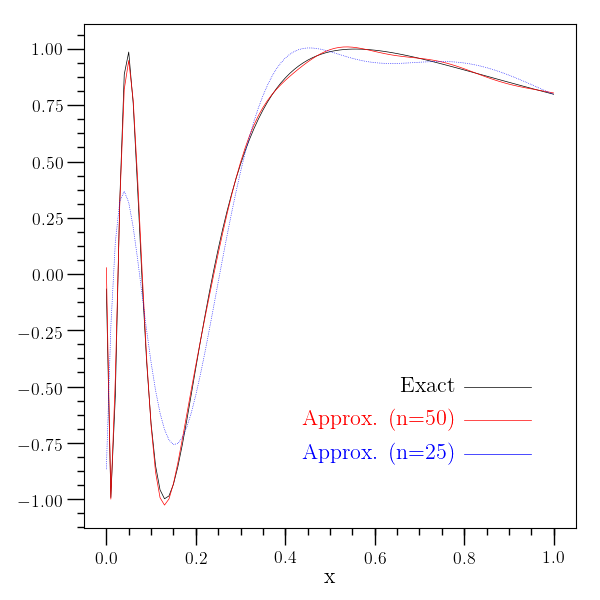
This example performs an approximation of the function \(y=\sin\left[ 1/\left(x+0.08 \right) \right]\) over \([0,2 \pi]\). This function oscillates strongly over this interval and requires a high order approximation to be accurate.

The image below shows the approximation for \(n=50\) \(n=25\). The \(n=100\) would be nearly indistinguishable from the exact result on this scale.

/* Example: ex_chebapp.cpp
   -------------------------------------------------------------------
*/
  
#include <iostream>
#include <o2scl/constants.h>
#include <o2scl/test_mgr.h>
#include <o2scl/cheb_approx.h>
#include <o2scl/deriv_cern.h>
#include <o2scl/inte_qag_gsl.h>

using namespace std;
using namespace o2scl;

double func(double x) {
  return sin(1.0/(x+0.08));
}

double dfunc(double x) {
  return -cos(1.0/(x+0.08))/pow(x+0.08,2.0);
}

// Simple function to output information to file for plotting
void write_file(cheb_approx &gc);

int main(void) {
  test_mgr t;
  t.set_output_level(1);

  cout.setf(ios::scientific);

  funct tf=func;

  cheb_approx gc;
  deriv_cern<> cd;
  inte_qag_gsl<> gi;

  double res, err;
  double x0=0.55;

  // Initialize the Chebyshev approximation
  gc.init(func,100,0.0,2.0*o2scl_const::pi);

  // Evaluate the approximation and compare with the exact result
  cout << "f(0.55)" << endl;
  cout << "Exact         : " << func(x0) << endl;
  gc.eval_err(x0,res,err);
  cout << "Approx (n=100): " << res << endl;
  cout << " Est. Error   : " << err << endl;
  cout << " Act. Error   : " << fabs(res-func(x0)) << endl;

  // Evaluate the approximation at lower order
  gc.eval_n_err(50,x0,res,err);
  cout << "Approx (n=50) : " << res << endl;
  cout << " Est. Error   : " << err << endl;
  cout << " Act. Error   : " << fabs(res-func(x0)) << endl;
  gc.eval_n_err(25,x0,res,err);
  cout << "Approx (n=25) : " << res << endl;
  cout << " Est. Error   : " << err << endl;
  cout << " Act. Error   : " << fabs(res-func(x0)) << endl;
  cout << endl;

  t.test_rel(gc.eval(x0),func(x0),1.0e-4,"eval");

  // Show how to use operator=() to create a new approximation
  cheb_approx gc2=gc;
  cout << "Using operator=(): " << gc2.eval(x0) << " " << func(x0) << endl;
  cout << endl;

  t.test_rel(gc2.eval(x0),gc.eval(x0),1.0e-10,"op=");

  // Show how to compute the derivative
  cheb_approx gc_deriv;
  gc.deriv(gc_deriv);

  cout << "f'(0.55)" << endl;
  cout << "Exact         : " << dfunc(x0) << endl;
  gc_deriv.eval_err(x0,res,err);
  cout << "Approx (n=100): " << res << endl;
  cout << " Est. Error   : " << err << endl;
  cout << " Act. Error   : " << fabs(res-dfunc(x0)) << endl;
  cd.deriv_err(x0,tf,res,err);
  cout << "Direct deriv  : " << res << endl;
  cout << " Est. Error   : " << err << endl;
  cout << " Act. Error   : " << fabs(res-dfunc(x0)) << endl;
  cout << endl;

  t.test_abs(res,dfunc(x0),1.0e-12,"deriv with deriv_cern");
  t.test_abs(gc_deriv.eval(x0),dfunc(x0),5.0e-3,"deriv with cheb");

  // Show how to compute the integral
  cheb_approx gc_integ;
  gc.integ(gc_integ);

  cout << "int(f,0,0.55)" << endl;
  gc_integ.eval_err(x0,res,err);
  cout << "Approx (n=100): " << res << endl;
  cout << " Est. Error   : " << err << endl;
  gi.integ_err(tf,0.0,x0,res,err);
  cout << "Direct integ  : " << res << endl;
  cout << " Est. Error   : " << err << endl;
  cout << "Rel. Error    : " << fabs(res-gc_integ.eval(x0)) << endl;
  cout << endl;

  t.test_abs(gc_integ.eval(x0),gi.integ(tf,0.0,x0),1.0e-6,"integral");

  write_file(gc);
  
  t.report();
  return 0;
}
// End of example

// Simple function to output information to file for plotting
void write_file(cheb_approx &gc) {

  ofstream fout;
  fout.open("ex_chebapp.out");
  fout.setf(ios::scientific);
  
  for(double x=0.0;x<1.0001;x+=0.01) {
    fout << x << " " << func(x) << " " << gc.eval(x) << " "
	 << gc.eval_n(50,x) << " " << gc.eval_n(25,x) << endl;
  }

  fout.close();

  return;
}